Shells are such pleasurable natural sculptures that I bet there’s scarcely a bathroom in Britain whose shelf doesn’t boast at least one of them. I’ve often fiddled around sewing embroidered sketches – see the embroidered nautilus shell pictured above but have never ended up making them into something that satisfies me. I did once make a crepe de chine shirt with a shell embroidered asymmetric front and embroidered cuffs but until I’ve dyed the shell pink fabric a colour more like mushroom or stone, I won’t be blogging about it. Shell pink is after all only really suitable for shells or babies and little girls. Some lessons you earn the hard way.
Shells are not only very beautiful in themselves but they also beautiful mathematically. Growth spirals or logarithmic spirals are often seen in nature and were first described by René Descartes. Christopher Wren also noticed the logarithmic curve of the nautilus shell. Such spirals solve the problem of permitting growth yet retaining the same shape. In the case of the nautilus shell, the growing soft bodied animal needs a new hard whorl of shell every so often and this is done by scaling each successive whorl up by a constant factor – a relative change in just one factor has the required effect. .
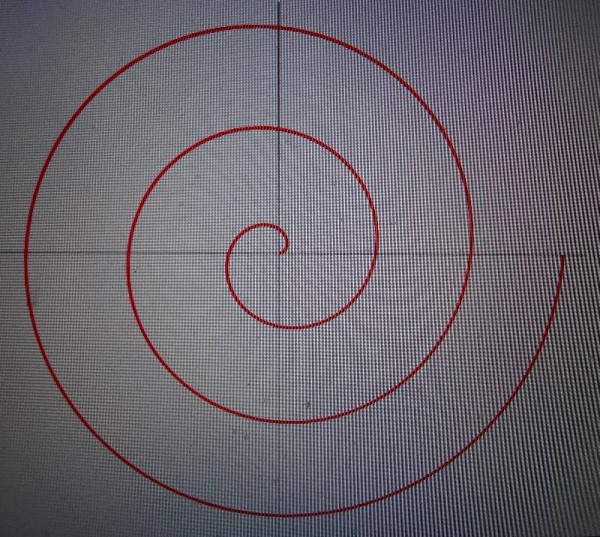
To try to make this clearer, look at the above spiral, also known as the Archimedean spiral. Here the distance between turnings is constant. Spirals such as these are used in watch balance springs and in very early gramophone records.
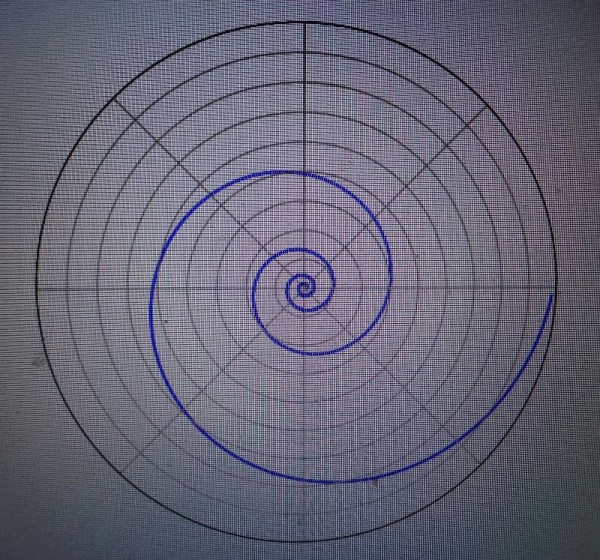
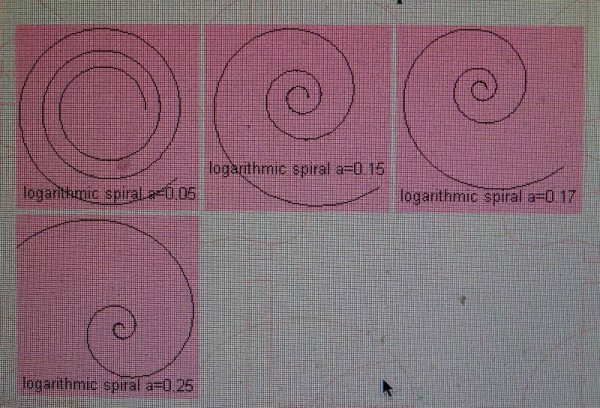
Now look at the next diagram and from it you can see the distance between turnings is now not constant. In fact it follows the pattern of a geometric progression but you don’t need to know this to see the difference in the two diagrams. You can see quite clearly that in the second diagram the turnings to the centre get tighter quicker. (A geometric progression is a sequence of numbers where each term is formed by multiplying the one before by a fixed number of constant, e.g. the series 2, 4, 8, 16, 32 which has a constant of 2.)
This curve is also known as the Fibonacci spiral. But whatever you call it, it explains many natural phenomena to which we never give a second thought. Hawks approach prey in this manner, as insects do to light sources. The arms of spiral galaxies are so described, which are visibly like the diagram when you think about it and with the same logic this also describes bands of tropical cyclones or even low pressure cells over Iceland. Apparently nerves of the cornea are also arranged in this pattern as are seeds on a sunflower head.
And that brings me back to my unfinished embroidery for which I’m no nearer finding a use. Perhaps I should just embroider the caption “The right kind of shell” (in a sort of take on Marcel Duchamp) frame it and keep it for daughter No 2 who is head of MAG in Vietnam and spends her days finding and blowing up shells of a much more unpleasant variety.



2 Comments
hi did you find a use for it?
Yes, I made it into a present for someone who lives by the sea and I blogged about it here http://www.addisonembroideryatthevicarage.co.uk/2015/09/03/dl-monogram-with-shell/
One Trackback
[…] example of a logarithmic spiral exemplifying the Fibonacci series that you can meet in nature (blogged about here with diagrams if you’re interested!) And with that I just about dried up with anything […]